38. PYTHON 알고리즘 - 성능 분석하기
알고리즘 사용 시 만족사항 3가지
- 알고리즘은 정확해야한다. 문제에 적절한 답을 줄 수 없는 알고리즘은 그다지 도움이 되지 않습니다.
- 알고리즘은 우리가 이해할 수 있어야 한다. 아무리 좋은 알고리즘이라도 너무 복잡하여 컴퓨터로 구현하기 어렵다면 쓸모가 없다.
- 알고리즘은 효율적이어야 한다. 알고리즘이 도출한 결과가 아무리 정확하더라도 이를 출력하는데 천년이 걸리거나 10억 테라바이트의 메모리가 필요하다면 문제 해결에 적합하지 않다.
공간 복잡도 분석 : 알고리즘을 실행하는 데 필요한 런타임 메모리 크기를 추정합니다.
시간 복잡도 분석 : 알고리즘을 실행하는데 걸리는 시간을 추정합니다.
성능 추정 - 최상의 경우
최상의 경우는 알고리즘이 최고의 성능을 낼 수 있도록 입력 데이터가 정리된 경우이다. 최산의 경우를 분석해 성능의 상한선을 확인할 수 있다.
성능 추정 - 최악의 경우
알고리즘의 성능을 추정할 수 있는 두번쨰 방식은 작업을 완료하는 데 걸리는 시간이 최대가 되는 경우이다. 최악의 경우를 분석해 알고리즘이 가진 선능의 하한선을 확인할 수 있다. 어떠한 악조건에서도 알고리즘은 최저 수준보다는 항상 나은 성능을 보이도록 보장되어 있습니다. 최악의 경우 분석은 특히 대규모 데이터를 가진 복잡한 문제에 대한 알고리즘 성능을 측정할 때 유용하다.
성능 추정 - 평균의 경우
1. 데이터를 그룹으로 나누고
2. 그룹의 대표적인 데이터를 성능 분석을 수행
3. 마지막으로 그룹별 결과를 모아 전체 평균을 계산한다.
평균의 분석은 알고리즘에 투입하는 입력데이터의 다양한 조합과 가능성을 고려해야 하기 때문에 항상 정확하지 않을 수 있으며 실행하기 어렵다는 단점이 있습니다.
빅오 표기법
빅오 표기법은 알고리즘의 성능을 정량화하는 도구로써 최악의 경우 분석에 널리 사용되고 있다.
상수 시간 복잡도 O(1)
입력 데이터의 크기에 관계없이 알고리즘의 시행 시간이 동일하다면 실행에 상수 시간이 소요된다고 하며 O(1)로 표기한다.
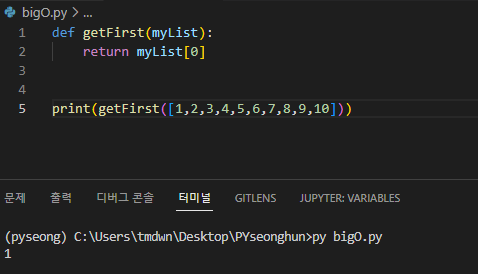
상수 시간이 소요되는 작업은 다음과 같다.
- push로 스택에 새 요소를 추가하거나 pop으로 스택에서 요소를 제거하는 작업
- 해시 테이블에 담긴 요소에 접근하는 작업
선형 시간 복잡도
알고리즘의 실행시간이 입력 크기에 비례한다면 이를 선형 시간 복잡도라고 하며 O(n)으로 표기한다.
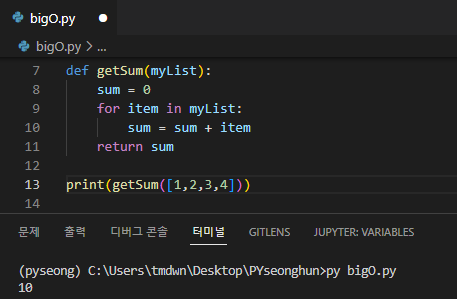
위의 식에서 for 문을 보면 myList의 크기(n)가 증가할 때마다 루프를 순회하는 횟수가 증가한다. 따라서 이 함수의 복잡도는 O(n)이다.
선형 시간 복잡도를 가지는 작업은
- 일차원 배열에서 요소를 검색하는 작업
- 일차원 배열에서 가장 작은 값을 가진 요소를 찾아내는 작업
이차 시간 복잡도 O(n^2)
입력 데이터 크기의 제곱에 비례하여 실행 시간이 증가하는 알고리즘은 이차 시간 복잡도를 가진다.
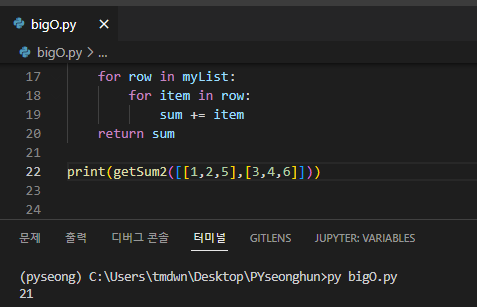
하나의 for 루프 안에 또 다른 루프가 들어 있다. 이렇게 중첩된 루프는 O(n^2)의 복잡도를 가진다.
이차 시간 복잡도를 가지는 또 다른 사례는 버블 정렬 알고리즘이 있다.
로그시간 복잡도 O(logn)
알고리즘의 실행 시간이 입력데이터의 크기에 로그를 취한 값에 비례한다면 로그 시간 복잡도를 가진다고 표현한다.

이진 검색 함수는 배열이 미리 정렬되어 있다는 점을 충분히 활용한다. 루프를 순회할 떄마다 검색할 배열의 크기를 절반씩 줄여 나간다. 위는 배열안에 특정한 값이 존재하는지 이진 검색으로 확인한 결과이다.
네 가지 빅오 표기법을 보았다.
입력데이터의 크기에 비례하여 실행 시간이 증가하는 유형중 최악의 성능은 O(N^2)이고 최고의 성능은 O(logN)이다. O(logN)의 성능은 항상 달정할 수 있는 것은 아니지만 모든 알고리즘 성능의 기준이라 할 수 있다.
그에반해 O(N^2) 는 O(N^3)보다는 성능이 낫지만, 이 유형으로 분류되는 알고리즘은 주어진 시간내에 처리할 수 있는 데이터양이 제한되어 있기 때문에 대규모 데이터를 다루는 데는 적합하지 않다.
근사알고리즘
알고리즘의 복잡도를 줄이는 방법중 하나는 정확도를 희생하는 것이다. 이러한 유형의 알고리즘을 근사 알고리즘이라고 한다.